Οι μεγάλες αποφάσεις μπορεί να φαίνονται συντριπτικές—ειδικά όταν η απόφαση είναι σημαντική και οι επιλογές σάς φαίνονται ατελείωτες. Πρέπει να συνεχίσετε να ψάχνετε ή να αρκεστείτε σε αυτό που είναι μπροστά σας; Παραδόξως, τα μαθηματικά έχουν μια απάντηση που θα μπορούσε να «σηκώσει» αυτό το βάρος από τους ώμους σας. Είναι ένας αντιδιαισθητικός αλλά ισχυρός κανόνας που ίσως αλλάξει τον τρόπο που προσεγγίζετε τα όσα σας προβληματίζουν, από τις σχέσεις σας μέχρι τις επαγγελματικές σας ευκαιρίες. Μάθετε πώς μπορείτε να αποφασίσετε πιο εύκολα αξιοποιώντας τον κανόνα του 37%.
Η ιαπωνική τεχνική για να διώξετε το στρες και να είστε ευτυχισμένοι
Ποιος είναι ο κανόνας του 37% και πώς μπορείτε να τον αξιοποιήσετε για να βρείτε λύση στα προβλήματά σας
Η ζωή είναι γεμάτη αποφάσεις που καθορίζουν την πορεία σας—από το να επιλέξετε σύντροφο, διαμέρισμα, δουλειά ή ακόμα και πού θα πάτε διακοπές—και το βάρος των υπερβολικά πολλών επιλογών μπορεί να μας αφήσει να νιώθουμε παγιδευμένοι, γεμάτοι αμφιβολίες ή σαν να συμβιβαζόμαστε. Αλλά τι θα γινόταν αν υπήρχε ένας μαθηματικός τύπος που να μπορούσε να σας βοηθά να πάρετε την καλύτερη απόφαση;
Σύμφωνα με τους μαθηματικούς, υπάρχει—και όλα συνοψίζονται σε κάτι που ονομάζεται «Κανόνας του 37%». Βασισμένη στη θεωρία πιθανοτήτων και το διάσημο «Πρόβλημα της Γραμματέως», αυτή η απατηλά απλή στρατηγική ίσως προσφέρει τον πιο ορθολογικό τρόπο για να πλοηγηθείτε στις μεγαλύτερες αποφάσεις της ζωής. Πριν αποδεχθείτε κάτι, πριν υπογράψετε ένα συμβόλαιο ή πριν κάνετε μια προσφορά, αφήστε τα μαθηματικά να σας δείξουν πότε να σταματήσετε να ψάχνετε και πότε να αρχίσετε να επιλέγετε.
Μελέτη: Πώς παίρνουμε αποφάσεις κάτω από δύσκολες συνθήκες
Το άρθρο του 2023 με τίτλο «Decision Making: Models, Processes, Techniques» παρέχει μια εκτενή εξέταση του πώς διαμορφώνονται και διαχειρίζονται οι αποφάσεις σε διάφορους τομείς, συμπεριλαμβανομένων των επιχειρήσεων, της ψυχολογίας και της επιστήμης υπολογιστών.
Τονίζει ότι η λήψη αποφάσεων είναι μια δομημένη διαδικασία με διακριτά βήματα—ξεκινώντας από τον ορισμό του προβλήματος και τη θέσπιση στόχων, έως την αξιολόγηση και επικύρωση εναλλακτικών. Το άρθρο ταξινομεί τα μοντέλα λήψης αποφάσεων σε κανονιστικά (ορθολογικά, με βάση τη μεγιστοποίηση της ωφέλειας) και περιγραφικά (φυσικά, βασισμένα στην εμπειρία), και συζητά περαιτέρω τα μοντέλα ορθολογικότητας έναντι περιορισμένης ορθολογικότητας για την αντιμετώπιση των προκλήσεων του χρόνου, των πληροφοριών και των γνωστικών περιορισμών.
Σημειώνει, επίσης, ότι η λήψη αποφάσεων σπάνια είναι απολύτως ορθολογική στην πράξη, καθώς επηρεάζεται συχνά από ψυχολογικούς, πολιτιστικούς και κοινωνικούς παράγοντες. Η μελέτη επισημαίνει επίσης τον αυξανόμενο ρόλο τεχνολογιών όπως η τεχνητή νοημοσύνη και η μηχανική μάθηση στη βελτίωση της ποιότητας των αποφάσεων παρέχοντας προγνωστικές πληροφορίες και μειώνοντας την προκατάληψη. Τελικά, λειτουργεί ως πολύτιμος οδηγός για άτομα και οργανισμούς που επιδιώκουν να βελτιώσουν τις ικανότητές τους στη λήψη αποφάσεων σε πολύπλοκα και αβέβαια περιβάλλοντα.
Ποια είναι τα «απλά» μαθηματικά πίσω από τις πιο δύσκολες αποφάσεις της ζωής μας
Η ζωή είναι γεμάτη μεγάλες αποφάσεις, και το να κάνετε μια επιλογή ανάμεσα σε φαινομενικά ατελείωτες επιλογές μπορεί να είναι – λοιπόν, παραλυτικά δύσκολο. Πρέπει να αγοράσετε αυτό το διαμέρισμα ή το άλλο; Να συγκατοικήσετε με αυτόν τον υποψήφιο συγκάτοικο ή με κάποιον άλλον; Να αρκεστείτε στον αρκετά καλό υποψήφιο ερωτικό σύντροφο ή να περιμένετε να δείτε αν θα εμφανιστεί ο «τέλειος» για εσάς; Είναι αρκετό για να σας κάνει να απελπιστείτε – αλλά μην φοβάστε: η επιστήμη έχει τη λύση.
Βελτιστοποιήσετε τις επιλογές σας
Όπως ένας ίσως απρόσμενος αριθμός μαθηματικών δεδομένων, αυτό έγινε διάσημο ως ένα παζλ «για διασκέδαση» που τέθηκε από τον Αμερικανό μαθηματικό Martin Gardner (τα υπόλοιπα, φυσικά, τέθηκαν από τον Άγγλο μαθηματικό John Conway).
Ήταν το έτος 1960, οπότε το αίνιγμα διατυπώθηκε ως «το Πρόβλημα της Γραμματέως» και πήγαινε κάπως έτσι:
- Υπάρχει μία μόνο θέση.
- Υπάρχει n αριθμός υποψηφίων για τη θέση και η τιμή του n είναι γνωστή.
- Οι υποψήφιοι, αν τους δούμε όλους μαζί, μπορούν να καταταγούν από τον καλύτερο στον χειρότερο με σαφήνεια.
- Οι υποψήφιοι παίρνουν συνέντευξη διαδοχικά με τυχαία σειρά, με κάθε σειρά να είναι εξίσου πιθανή.
- Αμέσως μετά από μια συνέντευξη, ο υποψήφιος με τον οποίο έγινε η συνέντευξη είτε γίνεται δεκτός είτε απορρίπτεται, και η απόφαση είναι αμετάκλητη.
- Η απόφαση αποδοχής ή απόρριψης ενός υποψηφίου μπορεί να βασιστεί μόνο στη σχετική κατάταξη των υποψηφίων που έχουν περάσει από συνέντευξη μέχρι στιγμής.
- Ο στόχος της γενικής λύσης είναι να υπάρχει η μεγαλύτερη πιθανότητα επιλογής του καλύτερου υποψηφίου από όλη την ομάδα. Αυτό είναι το ίδιο με τη μεγιστοποίηση της αναμενόμενης απολαβής, με την απολαβή να ορίζεται ως ένα για τον καλύτερο υποψήφιο και μηδέν σε αντίθετη περίπτωση.
Άλλες εκδοχές περιλάμβαναν το «πρόβλημα του αρραβωνιαστικού» (ίδια ιδέα, αλλά ψάχνετε για αρραβωνιαστικό αντί για γραμματέα) και το «παιχνίδι του googol» – σε αυτήν την έκδοση, γυρνάτε χαρτάκια για να αποκαλύψετε αριθμούς μέχρι να αποφασίσετε ότι μάλλον βρήκατε τον μεγαλύτερο απ’ όλους.
Όπως κι αν το παίξετε, η ερώτηση είναι η ίδια: πώς μπορείτε να μεγιστοποιήσετε την πιθανότητα να κάνετε την καλύτερη επιλογή;
Ο κανόνας του 37%
Διατυπωμένο με λόγια, αυτό είναι ένα περίπλοκο και δυσπρόσιτο πρόβλημα. Στα μαθηματικά, είναι αρκετά απλό.
«Αυτό το βασικό πρόβλημα έχει μία αξιοσημείωτα απλή λύση», έγραψε ο Αμερικανός μαθηματικός και στατιστικολόγος Thomas S Ferguson το 1989, σύμφωνα με το IFL Science. «Πρώτα, αποδεικνύεται ότι η προσοχή μπορεί να περιοριστεί στην κατηγορία κανόνων που, για κάποιον ακέραιο r > 1, απορρίπτουν τους πρώτους r – 1 υποψηφίους, και έπειτα επιλέγουν τον επόμενο υποψήφιο που είναι ο καλύτερος στη σχετική κατάταξη των υποψηφίων που έχετε δει».
Άρα, όταν αντιμετωπίζετε μία ροή από τυχαίες επιλογές και θέλετε να επιλέξετε την καλύτερη που σας προσφέρεται, το πρώτο πράγμα που πρέπει να κάνετε είναι… να απορρίψετε τους πάντες. Δηλαδή, μέχρι ένα σημείο – και μόλις φτάσετε σε αυτό το σημείο, απλώς επιλέξτε τον επόμενο υποψήφιο, σύντροφο ή χαρτάκι που είναι καλύτερος από οποιονδήποτε έχετε δει μέχρι εκείνη τη στιγμή.
Η ερώτηση τώρα είναι απλή: Πότε φτάνετε σε αυτό το σημείο για να ξεκινήσετε την απόρριψη;
Λοιπόν, ας πούμε ότι το σημείο διακοπής είναι ο υποψήφιος m – όλοι μέχρι τότε απορρίπτονται. Τώρα, αν ο καλύτερος υποψήφιος είναι ο m+1, συγχαρητήρια, θα τον δεχτείτε και θα έχετε την καλύτερη δυνατή πρόσληψη.
Αλλά τι γίνεται αν ο καλύτερος υποψήφιος είναι ο m+2; Λοιπόν, τότε υπάρχουν δύο τρόποι που μπορεί να εξελιχθεί αυτό: είτε ο m+1 ήταν καλύτερος από τους πρώτους m, αλλά όχι ο καλύτερος δυνατός, οπότε κρίμα, ατυχήσατε – δεν θα πάρετε τον καλύτερο υποψήφιο, γιατί ήδη επιλέξατε κάποιον που ήρθε πριν από τον καλύτερο – ή απορρίψατε τον m+1 και αποδεχτήκατε τον m+2.
Τώρα, φυσικά, θέλουμε το δεύτερο σενάριο, όχι το πρώτο – οπότε να τα καλά νέα: από όλες τις διατάξεις των πρώτων m+1 υποψηφίων, υπάρχουν μόνο 1/(m+1) σενάρια στα οποία θα αποδεχτείτε τον m+1 αντί για τον m+2. Αυτό σημαίνει ότι υπάρχουν ακόμα m/(m+1) σενάρια στα οποία περιμένετε και παίρνετε τον καλύτερο.
Ποια είδη μουσικής μας κάνουν ευτυχισμένους – Γιατί πρέπει να πηγαίνουμε σε συναυλίες
Εντάξει, οπότε τι γίνεται αν ο καλύτερος υποψήφιος βρίσκεται στη θέση m+3; Λοιπόν, αυτός θα γίνει αποδεκτός μόνο αν ούτε ο υποψήφιος m+1 ούτε ο m+2 ξεπερνούν όλους τους προηγούμενους – και αυτό συμβαίνει μόνο σε 2/(m+2) των περιπτώσεων. Και πάλι, αυτό σημαίνει ότι περιμένετε για τον καλύτερο σε m/(m+2) των περιπτώσεων.
Ίσως βλέπετε ήδη ένα μοτίβο: γενικά, αν ο n-οστός υποψήφιος είναι ο καλύτερος, θα γίνει αποδεκτός m/(n – 1) φορές από τις n – 1. Καθώς αφήνουμε το n να μεγαλώνει μέχρι το άπειρο, αυτό το μοτίβο γίνεται ένα όριο. «Η πιθανότητα, ϕ(r), να επιλεγεί ο καλύτερος υποψήφιος είναι 1/n για r = 1», εξηγεί ο Ferguson, «και, για r > 1 […] το άθροισμα γίνεται μία προσέγγιση Riemann σε ένα ολοκλήρωμα».
Τώρα η ερώτηση είναι: πώς μεγιστοποιούμε αυτή την τιμή; Και η απάντηση είναι στην πραγματικότητα αρκετά απλή: θέτετε το x ίσο με 1/e, που είναι περίπου 0,368.
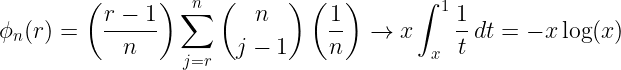
Λόγω του τρόπου που λειτουργούν οι λογάριθμοι και οι εκθέτες, αυτό σημαίνει ότι ϕ(r) = 0,367879… επίσης. Με άλλα λόγια, «είναι περίπου βέλτιστο να περιμένετε μέχρι να έχει γίνει συνέντευξη στο 37% των υποψηφίων περίπου και έπειτα να επιλέξετε τον επόμενο καλύτερο συγκριτικά», εξήγησε ο Ferguson. «Η πιθανότητα επιτυχίας είναι επίσης περίπου 37%». Αυτό ίσως να μην ακούγεται ιδιαίτερα εντυπωσιακό – είναι μόλις λίγο παραπάνω από μία στις τρεις πιθανότητες ότι θα βρείτε την καλύτερη δυνατή επιλογή, τελικά.
Αλλά όταν σκεφτείτε την εναλλακτική, είναι απίστευτο: «Αν επιλέγατε να μην ακολουθήσετε αυτή τη στρατηγική και αντ’ αυτού αποφασίζατε να καταλήξετε με έναν σύντροφο στην τύχη, θα είχατε μόνο μία πιθανότητα στις n να βρείτε την αληθινή σας αγάπη, ή μόλις 5% αν είναι πεπρωμένο σας να βγείτε με 20 άτομα στη ζωή σας, για παράδειγμα», έγραψε η Βρετανή μαθηματικός Hannah Fry, Καθηγήτρια της Δημόσιας Κατανόησης των Μαθηματικών στο University of Cambridge, στο βιβλίο της το 2015 The Mathematics of Love: Patterns, Proofs, and the Search for the Ultimate Equation.
«Αλλά απορρίπτοντας το πρώτο 37% των υποψηφίων εραστών σας και ακολουθώντας αυτή τη στρατηγική, μπορείτε να αλλάξετε δραματικά την τύχη σας, σε ένα εντυπωσιακό 38,42% για ένα πεπρωμένο με 20 πιθανούς εραστές».
Λειτουργεί πραγματικά ο κανόνας του 37%;
37%. Δεν έχει σημασία τι επιλέγετε ή πόσες επιλογές έχετε. Όλα συνοψίζονται σε αυτό το ποσοστό-κλειδί. Ακούγεται πολύ καλό για να είναι αληθινό, έτσι δεν είναι;
«Είμαι μαθηματικός και άρα προκατειλημμένη, αλλά αυτό το αποτέλεσμα κυριολεκτικά με αφήνει άναυδη», έγραψε η Fry. «Έχετε τρεις μήνες να βρείτε κάπου να μείνετε; Απορρίψτε τα πάντα τον πρώτο μήνα και μετά διαλέξτε το επόμενο σπίτι που εμφανίζεται και είναι το αγαπημένο σας μέχρι τώρα. Προσλαμβάνετε έναν βοηθό; Απορρίψτε το πρώτο 37% των υποψηφίων και μετά δώστε τη δουλειά στον επόμενο που προτιμάτε πάνω από όλους τους άλλους».
Λοιπόν, αν η λογική είναι ορθή, και τα μαθηματικά επιβεβαιώνονται – κάτι που ισχύει – γιατί αυτό το αποτέλεσμα αισθάνεται τόσο λάθος; Λοιπόν, όπως επισήμανε η Fry σε μία ομιλία TED το 2014, υπάρχουν κάποιες πραγματικές παγίδες που μπορεί να εμφανιστούν: «αυτή η μέθοδος συνοδεύεται από κάποιους κινδύνους», είπε. «Για παράδειγμα, φανταστείτε ότι ο τέλειος σύντροφός σας εμφανίζεται μέσα στο πρώτο 37%. Τώρα, δυστυχώς, θα πρέπει να τον απορρίψετε».
Αλλά «αν ακολουθείτε τα μαθηματικά», συνέχισε, «φοβάμαι ότι δεν εμφανίζεται κανένας άλλος που να είναι καλύτερος από οποιονδήποτε έχετε δει μέχρι τώρα, οπότε πρέπει να συνεχίσετε να απορρίπτετε τους πάντες, και να πεθάνετε μόνοι». Παρόλα αυτά, υπάρχει ένας τρόπος να το αποφύγετε: χαμηλώστε τα στάνταρ σας.
«Τα μαθηματικά υποθέτουν ότι σας ενδιαφέρει μόνο να βρείτε τον απόλυτα καλύτερο διαθέσιμο σύντροφο για εσάς», έγραψε η Fry. «Αλλά στην πραγματικότητα, πολλοί από εμάς θα προτιμούσαμε έναν καλό σύντροφο από το να είμαστε μόνοι, αν ο “ένας και μοναδικός” δεν είναι διαθέσιμος».
Οπότε, ναι, έχετε περίπου 37% πιθανότητα να βρείτε τον «έναν και μοναδικό» απορρίπτοντας το πρώτο 37% αυτών που έρχονται – αλλά τι γίνεται αν είστε εντάξει με το να βρείτε έναν από το top 5%, για παράδειγμα; Λοιπόν, σε αυτή την περίπτωση, το σημείο διακοπής σας είναι χαμηλότερο.
«Αν απορρίψετε τους συντρόφους που εμφανίζονται στο πρώτο 22% του παραθύρου ραντεβού σας και επιλέξετε το επόμενο άτομο που εμφανίζεται και είναι καλύτερο από οποιονδήποτε έχετε γνωρίσει πριν, θα καταλήξετε με κάποιον εντός του top 5% των πιθανών συντρόφων σας σε ένα εντυπωσιακό 57% των περιπτώσεων», εξήγησε η Fry.
Αποδεχθείτε οποιονδήποτε από το top15% των πιθανών υποψηφίων, και οι πιθανότητές σας ανεβαίνουν ακόμα περισσότερο. Τότε, το μόνο που χρειάζεται είναι να απορρίψετε το πρώτο 19% που έρχεται – και μπορείτε να αναμένετε σχεδόν τέσσερις στις πέντε πιθανότητα επιτυχίας. Και ας το παραδεχτούμε: όταν πρόκειται για την αγάπη, αυτές δεν είναι κακές πιθανότητες.
Πηγές: IFLScience, ResearchGate, Umass Dartmouth

